Provas de conhecimento zero: o que são zk-STARKs e como funcionam? (zk-Stark V2)

O que é Prova de Reservas e Prova de conhecimento zero?

Prova de Reservas (PoR)

Este é um processo para corretoras de criptomoedas mostrarem que têm ativos suficientes para cobrir todos os saldos dos clientes. A Prova de Reservas gera confiança ao provar que a corretora não está ocultando nenhum passivo. A maneira mais simples de fazer isso é publicando tanto o valor de ativos da corretora quanto uma lista de saldos de usuários para que todos possam conferir:

• O total de ativos em holding que a OKX afirma possuir é a soma do saldo total de ativos de cada usuário.

• O saldo total de cada usuário é superior a zero, e seus ativos são contabilizados, cobrindo seus passivos e garantindo que cada usuário tenha patrimônio líquido positivo.

• O valor total que a corretora declara abrange todos os usuários, permitindo que cada usuário verifique se seu valor líquido está incluído no total.

No entanto, revelar esses saldos pode comprometer a privacidade do usuário. Para resolver isso, usamos um método chamado Prova de conhecimento zero (ZKP - Zero Knowledge Proof) para proteger a privacidade do usuário.

Prova de conhecimento zero (ZKP)

É uma técnica de segurança que possibilita que a corretora de criptomoedas prove que uma afirmação é verdadeira sem revelar nenhuma informação adicional.

No nosso caso, queremos provar que temos fundos suficientes sem compartilhar detalhes específicos do usuário. A maioria dos ZKP se enquadra em duas categorias:

• zk-SNARK

• zk-STARK

Usamos zk-STARK porque é mais seguro e tem uma premissa de segurança mínima. Neste artigo, explicaremos como usamos zk-STARK para proteger a privacidade do usuário enquanto demonstramos nossa solvência.Antes de continuarmos, é importante entender alguns termos básicos de ZKP, como Circuito, árvore de Merkle e Compromissos.

Para iniciantes, existem muitos recursos disponíveis para ajudar você a começar. Para usuários experientes, você pode conferir o Curso MOOC e a monografia acadêmica.

Como o zk-STARK funciona?

Criamos uma árvore de Merkle usando o hash da conta de cada usuário como as folhas. Cada conta mostra saldos em USD para vários tokens (porexemplo, BTC, ETH) Para gerenciar esses saldos, os separamos em patrimônio que não seja negativo e dívida para cada token. Dessa forma trabalhamos apenas com números positivos, facilitando os cálculos e evitando erros.

Por exemplo:

• Se o saldo do token BTC de um usuário for A, seu patrimônio em BTC será A e a dívida em BTC será 0.

• Se o saldo do token ETH de um usuário for -B, seu patrimônio correspondente será 0 e a dívida será B

Em seguida, criaremos uma arvore de Merkle com esses valores de conta como folhas. A raiz da árvore atua como um valor único representando todos os saldos dos usuários. Cada usuário pode provar que sua conta faz parte dessa árvore usando um caminho de Merkle que mostra como sua conta se conecta à raiz.

Também publicamos o patrimônio total e a dívida somados de todos os tokens e usuários. Em seguida, criamos uma Prova de conhecimento zero (ZKP) para mostrar duas coisas:

• Prova de soma: os valores de patrimônio e dívida na árvore de Merkle são somam corretamente

• Prova não negativa: o patrimônio total de cada usuário é maior do que sua dívida total

Quando tentamos verificar a árvore de Merkle para um grande número de contas, se torna muito difícil lidar com tudo de uma vez. Para superar esse desafio, dividimos as contas em grupos menores chamados lotes. Cada lote é processado separadamente usando circuitos em lote, que verifica a parte inferior da árvore de Merkle.

Esses lotes facilitam o gerenciamento e também nos possibilitam executar essas verificações ao mesmo tempo (processamento paralelo). Uma vez que temos os resultados de cada lote, usamos outra camada de circuitos, chamada circuitos recursivos, para combinar e verificar todos os lotes juntos até que tenhamos conferido toda a árvore de Merkle.

O que é circuito em lote?

O circuito em lote recebe 1024 contas (acc₀, acc₁,..., acc₁₀₂₃) como entradas e gera três saídas principais: um hash (h_batch), um valor total de patrimônio (e_batch) e um valor total de dívida (d_batch). O que confirma que:

• O patrimônio total denominado em USD de cada conta é maior do que sua dívida total

• e_batch é a soma de todos os valores de patrimônio denominados em USD nessas contas

• d_batch é a soma de todos os valores de dívida denominados em USD nessas contas

• h_batch é a raiz da árvore de Merkle criada usando os hashes das contas

• Não há sobrecarga durante a soma para e_batch e d_batch

O que é circuito recursivo?

O circuito recursivo conta com 64 provas diferentes (π₀, ..., π₆₃), hashes (h₀, ..., h₆₃), patrimônios (e₀, ..., e₆₃₎ e dívidas (d₀, ..., d₆₃) dos circuitos da camada inferior como entradas. Ele combina essas entradas e produz três saídas: um novo hash (h_recursive), patrimônio total (e_recursive) e dívida total (d_recursive). O que confirma que:

• Cada uma das 64 provas é válida

• Cada prova π₀, ..., π₆₃ do circuito de camada inferior é válido

• e_recursive é a soma de e₀, ..., e₆₃

• d_recursive é a soma de d₀, ..., d₆₃

• h_recursive é o hash da concatenação de h₀, ..., h₆₃, porexemplo,

  • h_recursive = hash (h₀ || h₁ || ... || h₆₃₎

• Não há sobrecarga durante a soma para e_recursive e d_recursive

Qual é a relação entre circuitos em lote e circuitos recursivos?

O diagrama abaixo ilustra como o circuito em lote e os circuitos recursivos se conectam e trocam dados entre si. Tenha em mente que no diagrama duplicamos os circuitos para fins ilustrativos, mas na nossa implementação usamos apenas um circuito para cada camada.

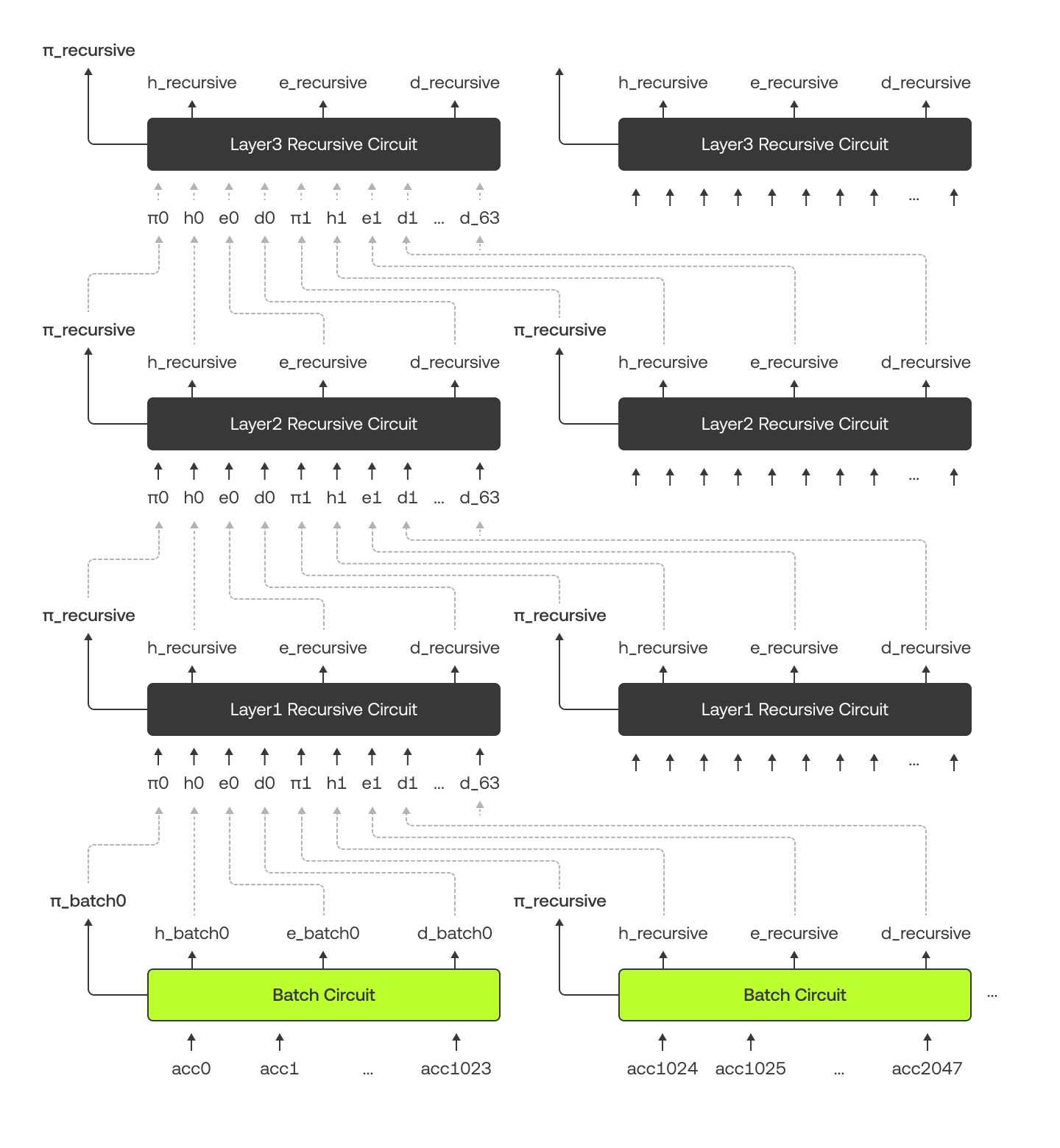
Nossa árvore de Merkle é estruturada de uma forma um pouco diferente. Nos 10 níveis inferiores, cada nó pai tem 2 filhos, enquanto nos níveis superiores, cada pai tem 64 filhos. Isto ocorre porque os circuitos em lote gerenciam a parte inferior e os circuitos recursivos gerenciam a parte superior. O diagrama abaixo usa um exemplo com "Alice" para mostrar a árvore de Merkle e sua prova de Merkle (em verde).

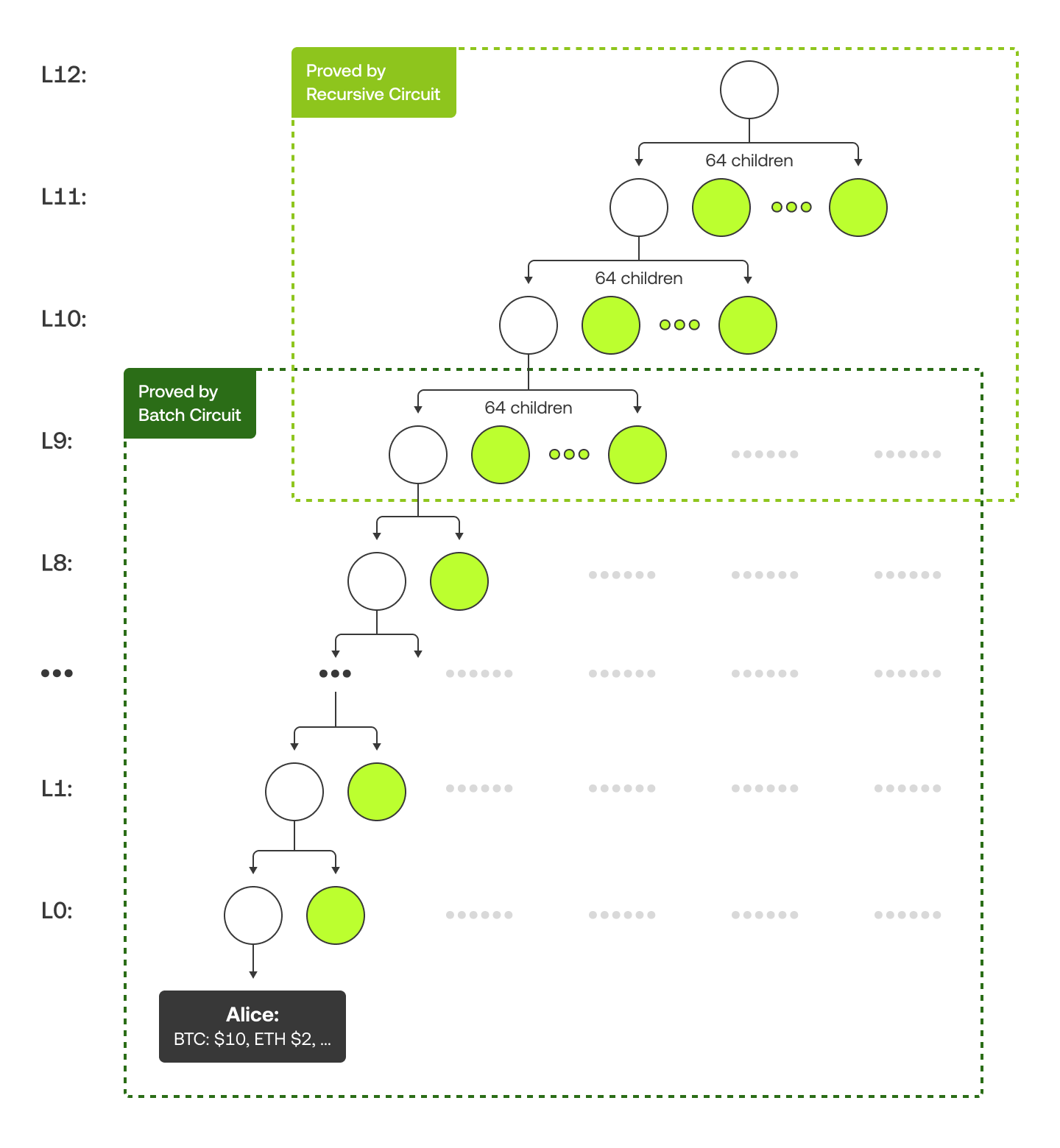
Para saber mais detalhes técnicos sobre como ajustamos os números das contas para se adequarem ao tamanho do lote ou escolhemos o algoritmo de hash correto, confira esta página.

Avanços na versão 2 do zk-PoR

Nossa versão 2 do zk-PoR fez vários avanços em relação à versão anterior:

• Maior eficiência: agora ele está 50 vezes mais rápido do que a versão anterior. Leva 3 horas em uma única máquina de 10 núcleos, em comparação com as 36 horas da versão anterior usando nove máquinas de 64 núcleos. Esse aumento de velocidade se deve ao uso da estrutura Plonky2, que compila circuitos codificados em Rust em uma linguagem de máquina eficiente, em vez de usar scripts Python mais lentos. Também aprimoramos o Plonky2 para executar alguns cálculos em GPUs, reduzindo o tempo em mais 30%.

• Auditoria facilitada: com a versão 2, usamos uma estrutura de alto nível que gerencia detalhes criptográficos complexos para nós. Isso torna nosso código mais simples, legível e menos propenso a erros.

• Prova concisa: o tamanho da prova da V2 (~500 KB) é apenas 0,05% da V1 (~1.2 GB). Graças ao método recursivo, as provas podem ser agregadas e condensadas repetidamente em uma única prova.

Como faço a autoverificação da Prova de Reservas (PoR)?

Saiba como você pode verificar se o saldo do seu ativo está incluído como uma folha da árvore de Merkle no zk-STARK:

1. Faça login na sua conta da OKX, navegue até Ativos e selecione Relatórios de PoR

2. Selecione Detalhes para visualizar seus dados de auditoria

   

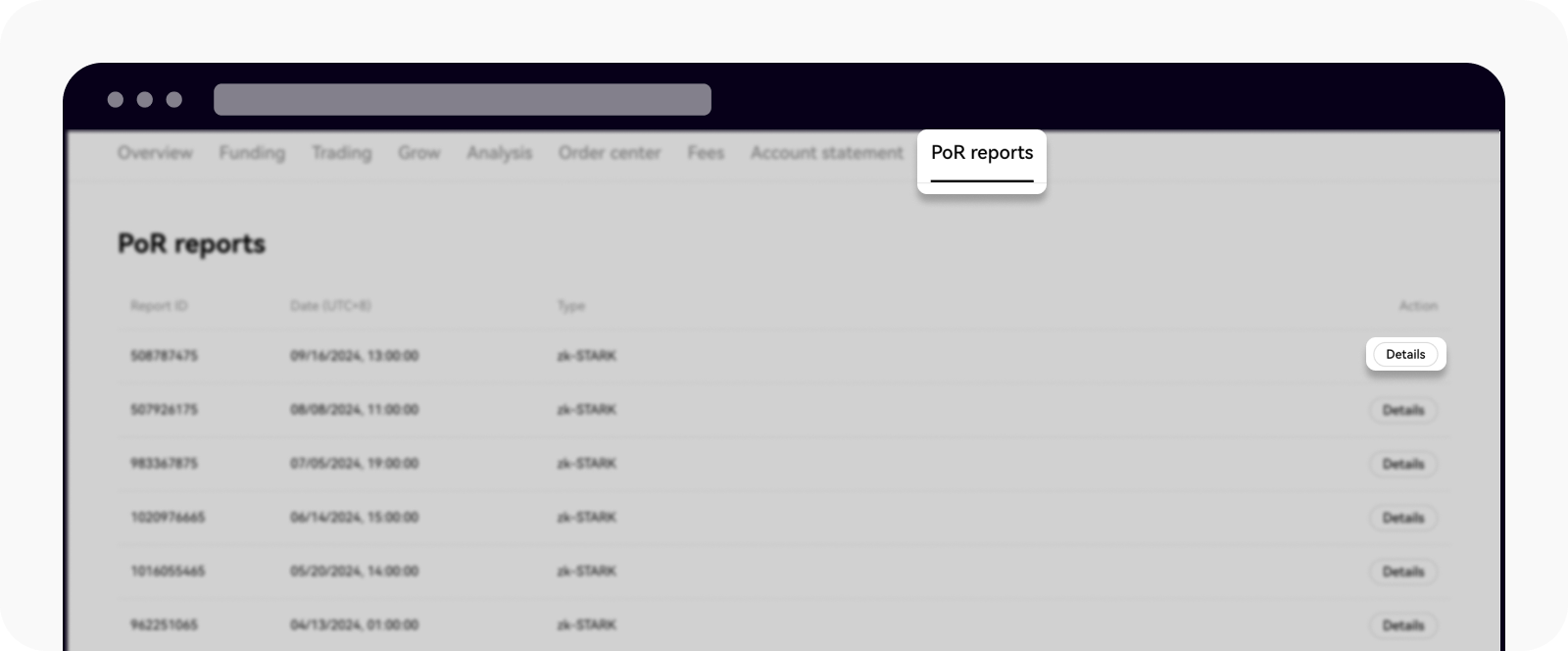
3. Obtenha os dados necessários para verificação manual ao selecionar Copiar dados

   

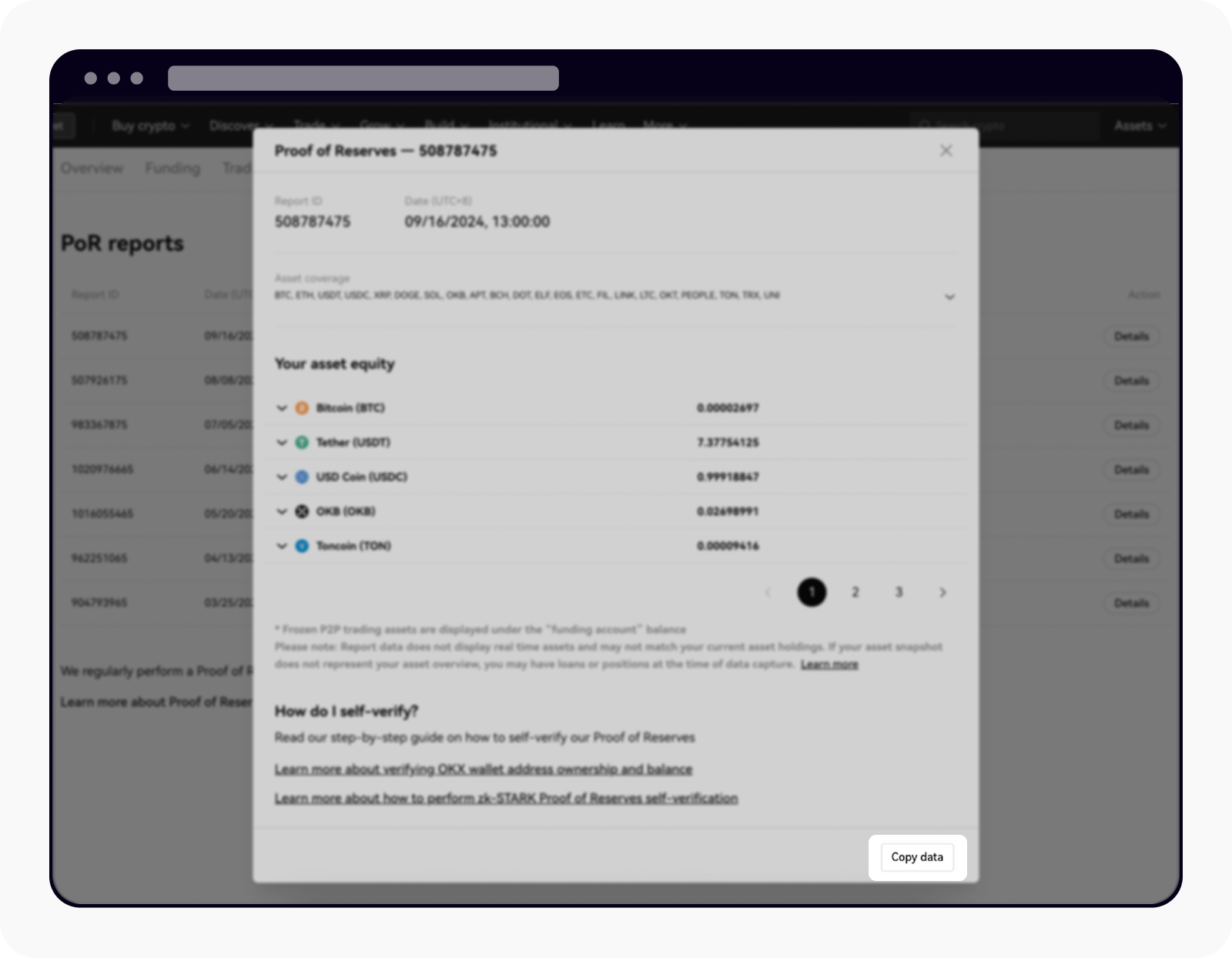
4. Depois de selecionar Copiar dados, abra o editor de texto (porexemplo, o bloco de notas) em seguida cole e salve a string JSON como um arquivo. O arquivo deve terminar com o nome "_inclusion_proof.json." A string JSON contém o saldo da sua conta e um snapshot do caminho de Merkle, salve o arquivo em uma nova pasta.

5. Abra um editor de texto (porexemplo, o bloco de notas) em seguida cole e salve a string JSON como um arquivo. O nome do arquivo deve terminar com "_inclusion_proof.json.", salve o arquivo em uma nova pasta.

   • A string JSON contém o saldo da sua conta e um snapshot do caminho de Merkle.

   • O texto JSON é mostrado abaixo:

     {"sum_tree_siblings":["9ffb169fecf075e203edca2af65e4c69fa4331d13ac75ccae4cd5b990c91b675","7149661a789763cb61293ebf5d8bdd5570e79ee203738f87a444c79642b89a79","788aac9e392fa62bc3f79c98c7afd7bb41ee7d5bd496876cd0580080f19e002f","e828a44d345e6799e232aabc57cb2b92986ee1c52b65344d83e79d84b4b571b7","6c0675de9cd6b2be1abd6a98260e7ea776492c4aa9aadf31086f23452cb7c48d","2dfe3aadb5ac00ee0b1110ee8c313afdee85d9f9c62904d6ee79c8f02354d80a","5068ae26192587432892a6de8b54ea25a8aafd1c010ab5e67b55b2c30c6257fa","a1bb026ec9f3d8a1fa1b6f498c40ed8b117a57e1af9816d08d9135ab4fe43a60","119dfcd214191405b7f7f7c7091b89196c0cae818bfcd8252a48f20d9cf3c378","4d9403482ca177c669df34a60bb2afab7a18097012d0b70703c8e59258cdfee6"],"recursive_tree_siblings":[{"right_hashes":["e041eaa366259f873e9e1477aac77362f4b1b460c2d5e1c14907fa9288d66cff","b45a8c503e649ff39543a918996b06fc65f4df9b61d071b22f7342f94862c9be","e00ec1225dfe6b7e950f6b9b8e9d1121bf17eb60c444fd7191b861a2ddddad23","c02c12beb73c03f996508cdce7bef927f0aa8b77ebd899f6a75df83de9d4022e","d36b95f14c5fd5bfaf1347e3177340e2fc9475a77b852321b80527132e7d539c","c0b9770178e70a7bba4ac8aeaadab2bcb2ae7f90d0f678bd463f2c42ff4f4a7b","fab5e7c6f7f8bc6d51f515c5db235cc1ebe987adee8c19c9bc7313e9e266d72c","b3884fb88fc95949c78ca8867cfa9e8a3c4c59fa1a48d8371f7fbfbebda0acfd","0c6da9bdbd40065f92ddaa45297670f2f0bffedb74020c5d5752e70d8b507b77","left_hashes":["1101beee3c6a36a168ceee9d43fcf6cb6de7e5c87ed4d22cd0308c9870d17839","d40a8e9eb4c873996ec515600def480eaa9378ca8481a7bcdf5f77725dbec4ae","63b12566ba8473f502386e92d500664cb63683dca6c26593378dcc9715257b77","166440a8ccbfbc1ce6ec5efaf8bc0b25e1bf692fa972e2729e45ce709d1d35a3","724451ad1d937fc47de5ede930d159dce78093d5e6a1f2e698452f8a29b4de3a","081a88f12d4e23173a1bf5038d4a9413cc92dd421c92261065de06492b5010ec","a76dbb1d4c393539b9546f4460d50ebc7582748d7de63c62c463b793c55bac7c","91e6c21de3f4060e1bd864131a570af42de31bbcd84a5afcbbc8fedcbf806002","fad08eca5bfdc5f37d39eabb44c2216afc6498afcb6b913d72586eaaf132a572","d39b06fe28387ba8045e2b2f95e90613916beef4f79df7961514e6e4cbfd07fa","81d07e300a116a0e4fcb56c39715c5fd5921abe8d10329b07c3f33d417b70ca8","7b72a7e62a45c9958a8a55eec2ba47352f2af701bacba098668589f6a3ce0423","8766bc64c38c2bb4188d89de0e732bca103daaed0c779cba9a8b191e24b51c9c","fa57ae4409e46c605f3cbfd01dfd9ccebc86cbd765cdc067206cb9367832442f"]}, ...... "index":9583119,"account":{"id":"50f5f08cc5036e15a541c64ac4ac6d2d9aa8ddab1ec32ed58b10e6ed3edfad59","debt":["0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0"],"equity":["8412384","9386185","45265193","0","0","8751","3824171","2716990","0","313671","28319","0","0","0","41261","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","142353","0","0","0","0","0","4435","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","662","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","993","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","25132","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","305","0","0","0","0","0","0","0","0","6141","0","0","0","0","0","0","0","0","0","0","0","5511","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0"]}}

6. Baixe a ferramenta de verificação de código aberto da OKX: zk-STARKValidator

7. Salve a ferramenta de verificação de código aberto da OKX, zk-STARKValidator, e o arquivo da string JSON juntos na nova pasta criada no passo 5. No nosso caso, colocamos a ferramenta e o arquivo de dados na pasta Downloads, com o nome de "proof-of-reserves”, conforme mostrado abaixo:

   

8. Abra o zk-STARKValidator, ele executará automaticamente o arquivo JSON que você salvou na pasta

9. Verifique o resultado:

   • Se a verificação for aprovada, será exibido o resultado Inclusion constraint validation passed:

     

   • Se a verificação falhar, será exibido o resultado Inclusion constraint validation failed:

     

Como faço para verificar o saldo total e a restrição não negativa do zk-STARK?

Saiba como você pode verificar se os ativos que afirmamos possuir são legítimos e que nenhum usuário possui patrimônio líquido negativo:

1. Navegue até a nossa página Prova de Reservas e selecione Relatório de passivo

2. Baixe o arquivo zk-STARK e salve-o em uma nova pasta

   

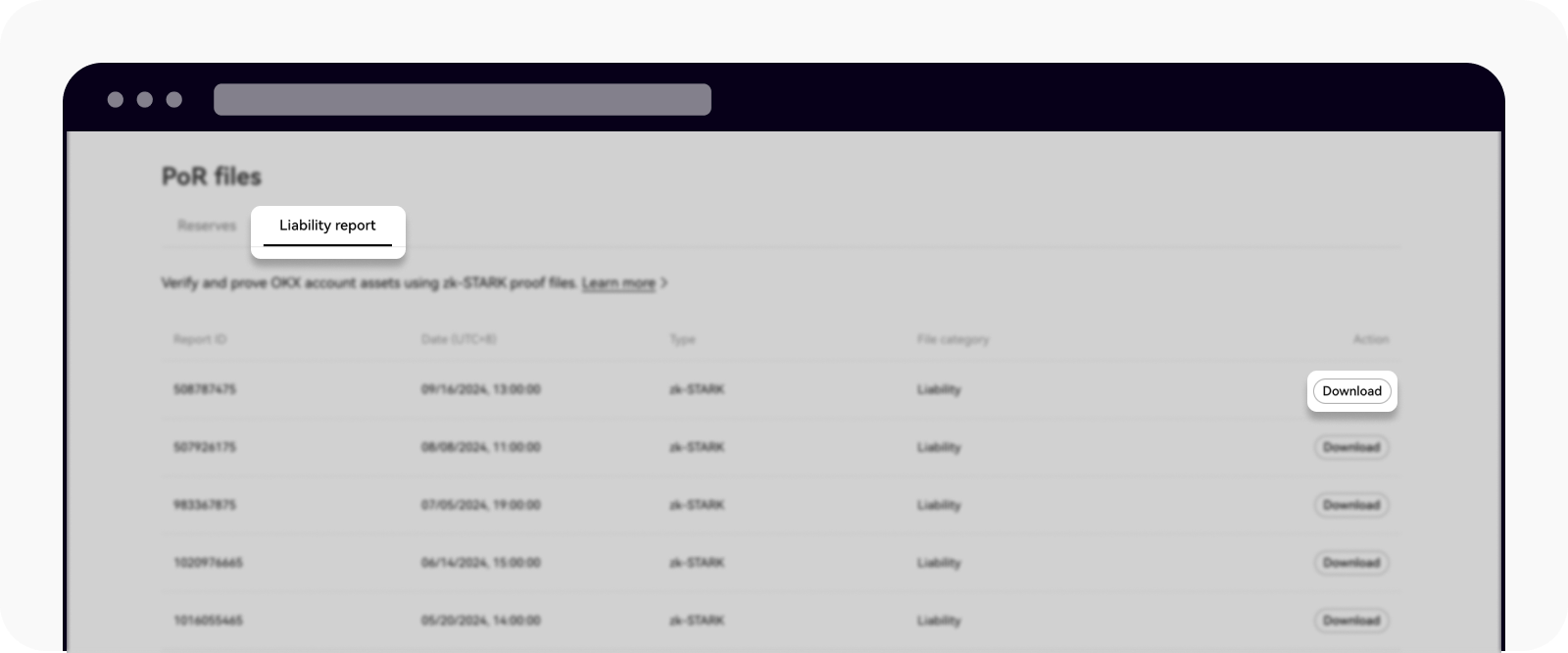
3. Descompacte o arquivo para extrair um arquivo “sum_proof_data.json”

   

4. Baixe a ferramenta de verificação de código aberto da OKX: zk-STARKValidator

5. Salve a ferramenta de verificação de código aberto da OKX, zk-STARKValidator, e o arquivo"sum_proof_data.json" juntos na nova pasta criada no passo 2. No nosso caso, colocamos a ferramenta e o arquivo de dados na pasta Downloads, com o nome de "proof-of-reserves”, conforme mostrado abaixo:

   

6. Abra o zk-STARKValidator, ele executará automaticamente o arquivo sum proof data que você salvou na pasta.

7. Verifique o resultado

   • Se a verificação for aprovada, será exibido o resultado Total sum and non-negative constraint validation passed:

     

   • Se a verificação falhar, será exibido o resultado Total sum and non-negative constraint validation failed:

     

Para explorar mais detalhes técnicos, nosso sistema de Prova de Reservas é de código aberto e está disponível para análise e uso no github.