Докази з нульовим розголошенням: що таке zk-STARKs і принцип роботи? (zk-Stark V2)
Що таке підтвердження резервів та доказ з нульовим розголошенням?
Підтвердження резервів (PoR)
Це те, як криптовалютні біржі доводять, що у них є достатньо активів для покриття всіх балансів клієнтів. На такому доказі, що біржа не приховує жодних зобов'язань, вибудовується довіра. Найпростіший спосіб показати це — опублікувати як обсяги активів біржі, так і залишки на акаунтах користувачів, щоб кожен міг перевірити:
Загальна сума активів користувачів, яку, як стверджує OKX, утримує на балансі, є сумою загального балансу активів кожного користувача.
Загальний баланс кожного користувача перевищує нуль, а їхні активи враховані, покриваючи їхні зобов'язання та гарантуючи, що кожен користувач має позитивний чистий капітал.
Загальна сума, за твердженням біржі, враховує кожного окремого користувача, тому кожен користувач повинен мати можливість перевірити, чи входить його сума чистої вартості в загальну вартість активів.
Однак інформація з цих акаунтів може скомпрометувати конфіденційність користувачів. Щоб вирішити це, ми використовуємо метод, так званий доказ з нульовим розголошенням (ZKP) для захисту конфіденційності користувачів.
Доказ з нульовим розголошенням (ZKP)
Це техніка безпеки, яка дозволяє криптовалютній біржі довести, що заява є правдивою, не розкриваючи жодної додаткової інформації.
У нашому випадку ми хочемо довести, що у нас достатньо коштів, не розкриваючи конкретні дані користувача. Більшість ZKP підпадає під дві категорії:
zk-SNARK
zk-STARK
Ми використовуємо zk-STARK, тому що він є безпечнішим і має мінімальний ризик. У цій статті ми пояснимо, як ми використовуємо zk-STARK для захисту конфіденційності користувачів, при цьому доводимо нашу платоспроможність.Перед тим, як продовжити, корисно зрозуміти деякі основні терміни ZKP, такі як схема, дерево Меркла та зобов'язання.
Для початківців є багато ресурсів, які допоможуть вам з початковим розумінням. Досвідчені користувачі можуть звернутися до MOOC курсу та академічної монографії.
Як працює zk-STARK?
Ми створюємо дерево Меркла, у якому замість листя використовуються хеші облікового запису кожного користувача. Кожен акаунт показує баланс в USD для різних токенів (наприклад, BTC, ETH). Щоб опрацювання цих балансів ми розділяємо їх на невід’ємну кількість капіталу та борги для кожного токена. Таким чином, ми працюємо лише з позитивними числами, що полегшує виконання обчислень і допомагає уникати помилок.
Наприклад:
Якщо баланс токенів BTC користувача дорівнює A, то його капітал у BTC дорівнює A, а борг у BTC дорівнює 0.
Якщо баланс токенів ETH користувача дорівнює -B, його відповідний капітал дорівнює 0, а борг дорівнює B.
Далі ми будуємо дерево Меркла з цими значеннями акаунтів як листям. Корінь дерева є єдиним значенням, що представляє всі баланси користувачів. Кожен користувач може перевірити, що його акаунт є частиною цього дерева за допомогою шляху Меркла, який показує, як його акаунт під’єднується до коріння.
Ми також публікуємо загальний капітал і борг, підсумовані по всіх токенах і користувачах. Тоді ми створюємо доказ з нульовим розголошенням (ZKP), щоб показати дві речі:
доказ суми: значення капіталу та боргу в дереві Меркла сумуються правильно.
Доказ невід’ємних балансів: загальний капітал кожного користувача більший за його загальний борг.
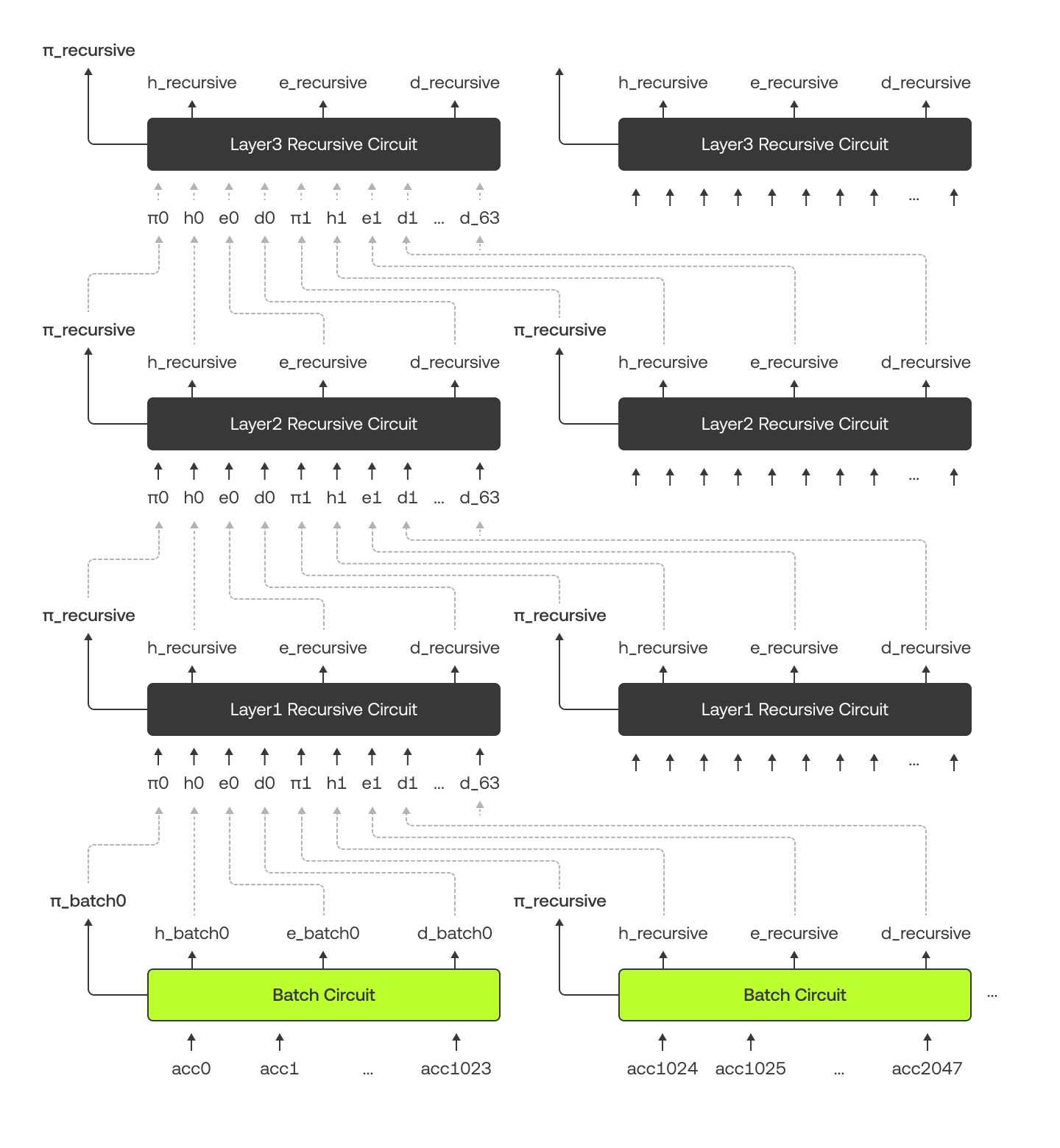
Коли ми намагаємося перевірити дерево Меркла для великої кількості акаунтів, то не можемо опрацювати їх за один раз. Щоб подолати цю проблему, ми розбиваємо облікові записи на менші групи, які називаються пакетами. Кожний пакет опрацьовується окремо за допомогою пакетних кіл, які перевіряють нижню частину дерева Меркла.
З пакетним опрацюванням це стає не лише можливим, але й дозволяє нам виконувати ці перевірки одночасно (паралельне опрацювання). Щойно ми отримаємо результати з кожного пакету, ми перейдемо на іншу схему, яке називається рекурсивною, щоб об'єднати та перевірити всі пакети разом, поки не перевіримо все дерево Меркла.
Що таке пакетна схема?
Пакетна схема об’єднує 1024 акаунти (акаунт0, акаунт1,..., акаунт1023) як вхідні дані та генерує 3 основні результати: хеш (hbatch), загальна вартість капіталу (ebatch), та загальна вартість боргу (dbatch). В процесі перевіряється, що
загальний капітал у USD кожного акаунта перевищує його загальний борг.
ebatch — це сума всіх значень капіталу у USD на цих акаунтах.
dbatch є сумою всіх значень боргу USD на цих акаунтах
hbatch є коренем дерева Меркла, створеним за допомогою хешів акаунтів.
Під час підсумовування немає переповнення для ebatch та dbatch
Що таке рекурсивна схема?
Рекурсивна схема приймає 64 різні докази (π0, ..., π63), хеші (h0, ..., h63), капітал (e0, ..., e63), і борги (d0, ..., d63) з нижніх шарів як вхідні дані. Це поєднує ці вхідні дані та генерує 3 результати: новий хеш (hрекурсивний), загальний капітал (eрекурсивний) та загальний борг (dрекурсивний). В процесі перевіряється, що
Кожен з 64 доказів є дійсним
Кожний доказ π0, ..., π63 з нижнього шару схеми є дійсним
eрекурсивний є сумою e0, ..., e63
dрекурсивний є сумою d0, ..., d63
hрекурсивний є хешем об'єднання h0, ..., h63, i.тобто
hрекурсивний = Хеш (h0 || h1 || ... || h63)
Під час підсумовування немає переповнення для eрекурсивний та dрекурсивний
Яка взаємозв'язок між пакетними схемами та рекурсивними схемами?
Рисунок нижче ілюструє, як пакетна схема та рекурсивні схеми з'єднуються та передають дані між собою. Майте на увазі, що на рисунку ми дублюємо схеми для ілюстраційних цілей, але в нашій реалізації ми використовуємо лише одну схему для кожного шару.
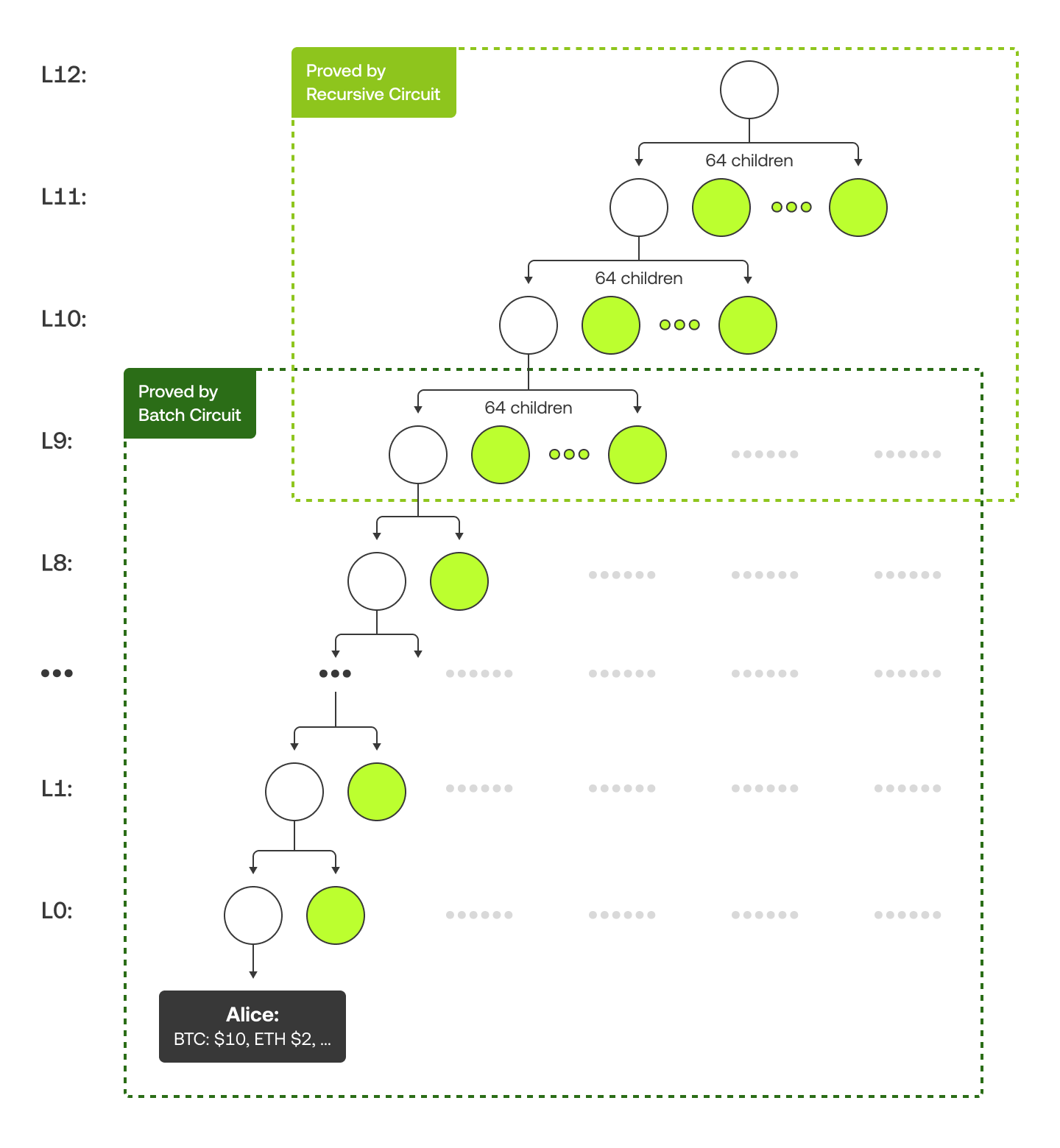
Наше дерево Меркла структуроване трохи інакше. На нижніх 10 рівнях кожна батьківська нода має 2 дітей, тоді як на верхніх рівнях — 64 дитини. Це пов'язано з тим, що пакетні схеми обробляють нижню частину, а рекурсивні схеми керують верхньою частиною. На рисунку нижче використовується приклад з Алісою, щоб показати дерево Меркла та її доказ Меркла (позначений зеленим кольором).
Для отримання більш технічних деталей, таких як те, як ми коригуємо номери акаунтів, щоб вони вміщувалися в пакет, або вибираємо правильний алгоритм хешування, перегляньте цю сторінку.
Вдосконалення у zk-PoR версії 2
У нашій версії 2 zk-PoR з’явилося кілька вдосконалень у порівнянні з попередньою версією:
Більша ефективність. Тепер вона у 50 разів швидша за попередню версію. Це займає 3 години на одному 10-ядерному комп'ютері, в порівнянні з 36 годинами попередньої версії, що використовує дев'ять 64-ядерних машин. Це прискорення зумовлене використанням фреймворку Plonky2, який компілює схеми, написані на Rust, в ефективну машинну мову замість використання повільніших скриптів на Python. Ми також вдосконалили Plonky2 для виконання деяких обчислень на графічних процесорах, зменшивши час на додаткові 30%.
Краща аудиторська перевірка. У версії 2 ми використовуємо високорівневий фреймворк, який опрацьовує складні криптографічні дані. Наш код стає зрозумілішим, читабельнішим і менш схильним до помилок.
Стислість. Розмір доказу V2 (~500 KБ) становить лише 0,05% від V1 (~1,2 ГБ). Завдяки рекурсивному методу докази можуть бути неодноразово агреговані та стиснуті в один доказ.
Як можна виконати самоперевірку підтвердження резервів (PoR)?
Ось як ви можете перевірити, чи включено ваш баланс активів як лист Меркла зі zk-STARK:
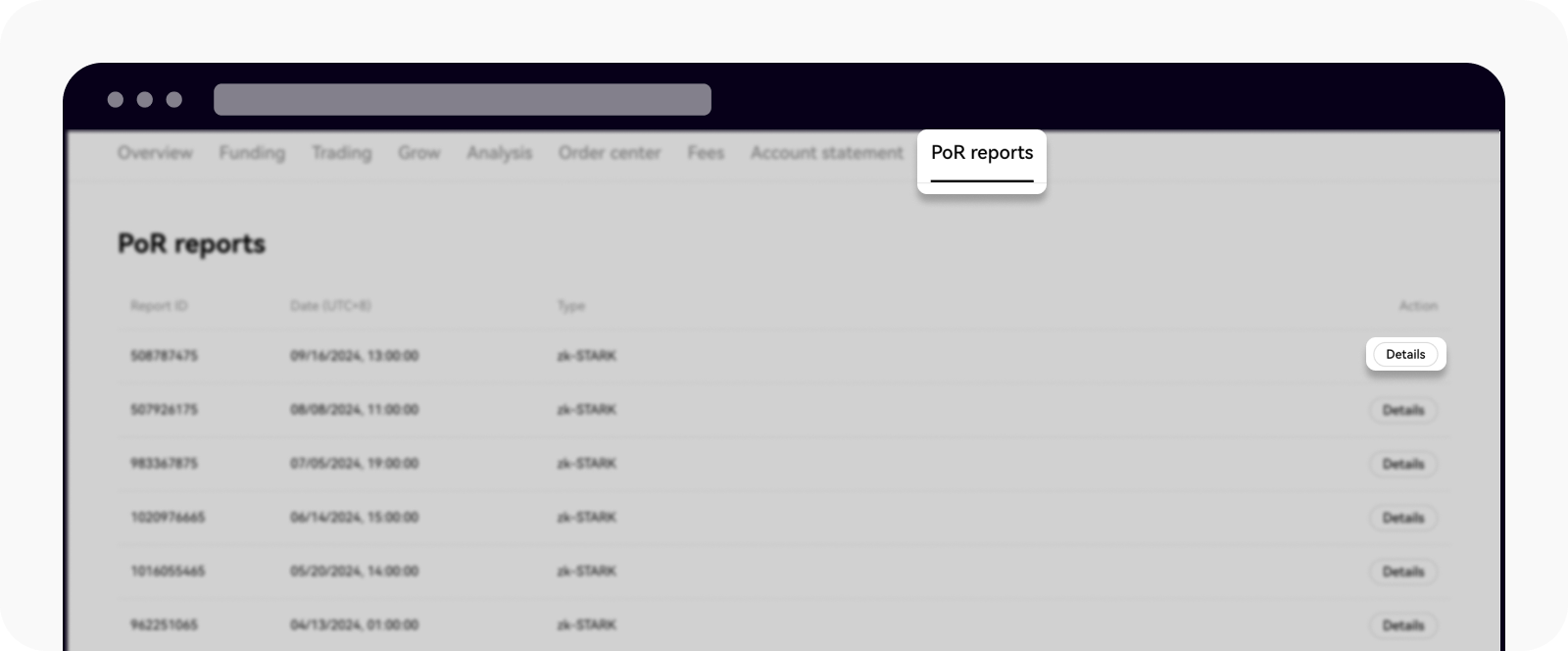
Увійдіть у свій акаунт OKX, перейдіть до Активи і виберіть звіти PoR
Виберіть Деталі, щоб переглянути ваші дані аудиту
Отримайте дані, які вам потрібні для ручної перевірки, вибравши Копіювати дані
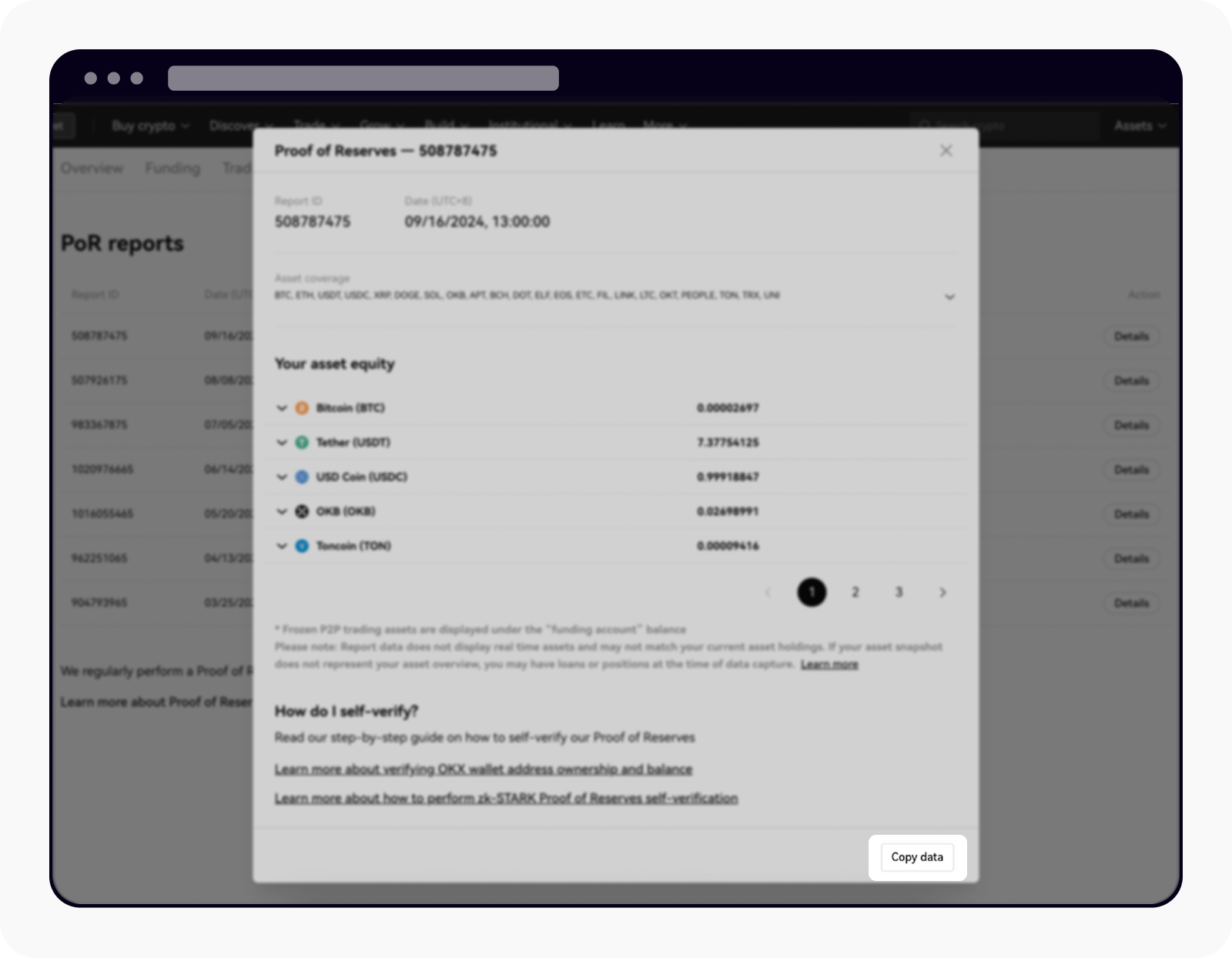
Після вибору Копіювати дані відкрийте текстовий редактор (наприклад, блокнот), потім вставте та збережіть рядок JSON як файл. Назва файлу повинна закінчуватися на "_inclusion_proof.json." Рядок JSON містить ваш баланс акаунта та знімок шляху Меркла, а потім файл зберігається у новій папці
Відкрийте текстовий редактор (наприклад,, блокнот), потім вставте та збережіть рядок JSON як файл. Назва файлу повинна закінчуватися на "_inclusion_proof.json." Збережіть файл у новій папці
Рядок JSON містить ваш баланс акаунта та знімок шляху Меркла.
Текст JSON показано нижче:
{"sum_tree_siblings":["9ffb169fecf075e203edca2af65e4c69fa4331d13ac75ccae4cd5b990c91b675","7149661a789763cb61293ebf5d8bdd5570e79ee203738f87a444c79642b89a79","788aac9e392fa62bc3f79c98c7afd7bb41ee7d5bd496876cd0580080f19e002f","e828a44d345e6799e232aabc57cb2b92986ee1c52b65344d83e79d84b4b571b7","6c0675de9cd6b2be1abd6a98260e7ea776492c4aa9aadf31086f23452cb7c48d","2dfe3aadb5ac00ee0b1110ee8c313afdee85d9f9c62904d6ee79c8f02354d80a","5068ae26192587432892a6de8b54ea25a8aafd1c010ab5e67b55b2c30c6257fa","a1bb026ec9f3d8a1fa1b6f498c40ed8b117a57e1af9816d08d9135ab4fe43a60","119dfcd214191405b7f7f7c7091b89196c0cae818bfcd8252a48f20d9cf3c378","4d9403482ca177c669df34a60bb2afab7a18097012d0b70703c8e59258cdfee6"],"recursive_tree_siblings":[{"right_hashes":["e041eaa366259f873e9e1477aac77362f4b1b460c2d5e1c14907fa9288d66cff","b45a8c503e649ff39543a918996b06fc65f4df9b61d071b22f7342f94862c9be","e00ec1225dfe6b7e950f6b9b8e9d1121bf17eb60c444fd7191b861a2ddddad23","c02c12beb73c03f996508cdce7bef927f0aa8b77ebd899f6a75df83de9d4022e","d36b95f14c5fd5bfaf1347e3177340e2fc9475a77b852321b80527132e7d539c","c0b9770178e70a7bba4ac8aeaadab2bcb2ae7f90d0f678bd463f2c42ff4f4a7b","fab5e7c6f7f8bc6d51f515c5db235cc1ebe987adee8c19c9bc7313e9e266d72c","b3884fb88fc95949c78ca8867cfa9e8a3c4c59fa1a48d8371f7fbfbebda0acfd","0c6da9bdbd40065f92ddaa45297670f2f0bffedb74020c5d5752e70d8b507b77","left_hashes":["1101beee3c6a36a168ceee9d43fcf6cb6de7e5c87ed4d22cd0308c9870d17839","d40a8e9eb4c873996ec515600def480eaa9378ca8481a7bcdf5f77725dbec4ae","63b12566ba8473f502386e92d500664cb63683dca6c26593378dcc9715257b77","166440a8ccbfbc1ce6ec5efaf8bc0b25e1bf692fa972e2729e45ce709d1d35a3","724451ad1d937fc47de5ede930d159dce78093d5e6a1f2e698452f8a29b4de3a","081a88f12d4e23173a1bf5038d4a9413cc92dd421c92261065de06492b5010ec","a76dbb1d4c393539b9546f4460d50ebc7582748d7de63c62c463b793c55bac7c","91e6c21de3f4060e1bd864131a570af42de31bbcd84a5afcbbc8fedcbf806002","fad08eca5bfdc5f37d39eabb44c2216afc6498afcb6b913d72586eaaf132a572","d39b06fe28387ba8045e2b2f95e90613916beef4f79df7961514e6e4cbfd07fa","81d07e300a116a0e4fcb56c39715c5fd5921abe8d10329b07c3f33d417b70ca8","7b72a7e62a45c9958a8a55eec2ba47352f2af701bacba098668589f6a3ce0423","8766bc64c38c2bb4188d89de0e732bca103daaed0c779cba9a8b191e24b51c9c","fa57ae4409e46c605f3cbfd01dfd9ccebc86cbd765cdc067206cb9367832442f"]}, ...... "index":9583119,"account":{"id":"50f5f08cc5036e15a541c64ac4ac6d2d9aa8ddab1ec32ed58b10e6ed3edfad59","debt":["0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0"],"equity":["8412384","9386185","45265193","0","0","8751","3824171","2716990","0","313671","28319","0","0","0","41261","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","142353","0","0","0","0","0","4435","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","662","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","993","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","25132","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","305","0","0","0","0","0","0","0","0","6141","0","0","0","0","0","0","0","0","0","0","0","5511","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0","0"]}}
Завантажте інструмент перевірки з відкритим кодом OKX: zk-STARKValidator
Збережіть інструмент перевірки з відкритим кодом OKX, zk-STARKValidator, та файл з рядком JSON разом у новій папці, створеній на 5-му кроці. У нашому випадку ми розмістили інструмент і файл даних у папці Завантаження, яка називається «підтвердження резервів», як показано нижче:

Відкрийте zk-STARKValidator; він автоматично запустить JSON-файл, який ви зберегли в папці
Перевірте результат:
Якщо перевірку пройдено, з'явиться результат Перевірка обмеження включення пройшла:

Якщо перевірка не вдалася, з'явиться результат Перевірка обмеження включення не вдалася:

Як можна перевірити загальний баланс zk-STARK та невід’ємного обмеження?
Ось як ви можете перевірити, що активи, які як ми стверджуємо, у нас є, є справжніми, і що жоден користувач не має негативного чистого капіталу:
Перейдіть на сторінку Підтвердження резервів та виберіть Звіт про зобов'язання
Завантажте файл zk-STARK та збережіть його в новій папці
Розпакуйте файл, щоб витягти файл sum_proof_data.json

Завантажте інструмент перевірки з відкритим кодом OKX: zk-STARKValidator
Збережіть інструмент перевірки з відкритим кодом OKX, zk-STARKValidator та файл sum_proof_data.json разом у новій папці, створеній на кроці 2. У нашому випадку ми розмістили інструмент і файл даних у папці Завантаження, яка називається «підтвердження резервів», як показано нижче:

Відкрийте zk-STARKValidator; він автоматично запустить файл даних доказу суми, який ви зберегли в папці.
Перевірте результат
Якщо перевірку пройдено, з'явиться результат Перевірку загальної суми та невід’ємного обмеження пройдено

Якщо перевірка не вдалася, буде показано результат Перевірку загальної суми та невід’ємного обмеження не пройдено:

Щоб дізнатися більше про технічні деталі, наша система підтвердження резервів має відкритий код і доступна для перегляду та використання на github.






